https://learnopencv.com/depth-estimation-using-stereo-matching/
Depth Estimation Using Stereo Matching | LearnOpenCV #
Depth estimation is a critical task for autonomous driving. It's necessary to estimate the distance to cars, pedestrians, bicycles, animals, and obstacles.The popular way to estimate depth is LiDAR. However, the hardware price is high, LiDAR is sensitive t
learnopencv.com
위 글을 구글 번역기로 돌린 결과물
스테레오 매칭을 사용한 깊이 추정
깊이 추정은 자율 주행의 중요한 작업입니다. 자동차, 보행자, 자전거, 동물, 장애물까지의 거리를 추정하는 것이 필요합니다.
깊이를 추정하는 일반적인 방법은 LiDAR입니다. 그러나 하드웨어 가격이 비싸고 LiDAR는 비와 눈에 민감하므로 스테레오 카메라로 깊이 추정하는 더 저렴한 대안이 있습니다. 이 방법을 스테레오 매칭이라고도 합니다.
일반적으로 스테레오 매칭 이면의 아이디어는 매우 간단합니다.
수평 변위만 있는 동일선상의 광축을 가진 두 대의 카메라가 있습니다. 왼쪽 카메라 프레임의 모든 픽셀에 대해 오른쪽 카메라 프레임에서 해당 픽셀을 찾을 수 있습니다. 왼쪽과 오른쪽 프레임에서 이 점과 관련된 픽셀 사이의 거리를 알면 점의 깊이를 추정할 수 있습니다. 점의 깊이에서 알 수 있듯이 이 점의 이미지 사이의 거리에 반비례합니다. 이 거리를 시차라고 합니다.

스테레오 매칭을 위한 고전적인 접근 방식
디스패리티 추정에 대한 고전적인 접근 방식은 다음 단계로 구성됩니다.
- 이미지에서 특징을 추출하여 원시 색상 강도보다 더 가치 있는 정보를 얻고 포인트 매칭을 개선합니다.
- 왼쪽 및 오른쪽 특징 맵이 서로 다른 디스패리티 수준에서 어떻게 일치하는지 추정하기 위해 비용 볼륨을 구성합니다. 예를 들어 절대 강도 차이 또는 상호 상관을 사용할 수 있습니다.
- 디스패리티 계산 모듈을 사용하여 비용 볼륨에서 디스패리티를 계산합니다. 예를 들어, 왼쪽 및 오른쪽 특징 맵이 가장 잘 일치하는 불일치 수준을 찾는 무차별 대입 알고리즘이 될 수 있습니다.
- 초기에 예측된 디스패리티 맵이 너무 조잡한 경우 디스패리티를 세분화합니다.
스테레오 매칭을 위한 사전 딥 러닝 방법에 대한 개요를 제공하는 Scharstein과 Szeliski의 설문 조사를 참조할 수 있습니다.
스테레오 매칭을 위한 데이터 세트
데이터는 컴퓨터 비전에서 중요한 역할을 하므로 스테레오 매칭을 위한 데이터 세트에 대한 몇 마디:
- Middlebury 데이터 세트는 이 작업의 첫 번째 데이터 세트 중 하나입니다. 33개의 정적인 실내 장면이 포함되어 있습니다. 이 논문에서는 데이터 세트 수집에 대해 설명합니다.
- 960×540 해상도의 39,000개 이상의 스테레오 프레임을 포함하는 대규모 합성 SceneFlow 데이터 세트. 많은 저자들이 스테레오 매칭 신경망의 사전 훈련에 사용했습니다. 논문에 데이터 세트에 대한 자세한 설명이 있습니다.
- KITTI는 자율 주행 시나리오의 인기 있는 벤치마크입니다. 움직이는 차량에서 데이터를 수집하고 LiDAR로 깊이를 추정합니다.
스테레오 매칭을 위한 딥 러닝 기반 접근 방식
오늘날 딥 러닝 방법은 위에서 설명한 많은 단계를 종단 간 알고리즘으로 결합합니다. 가장 초기의 예는 GCNet입니다. StereoNet과 PSMNet은 같은 아이디어를 따릅니다. 우리는 PSMNet 접근 방식에 깊이 집중할 수 있습니다.
그림 1에서 빌딩 블록 목록을 볼 수 있습니다.

이 접근 방식은 공유 가중치가 있는 백본을 사용하여 왼쪽 및 오른쪽 이미지에서 특징을 추출합니다. 흥미롭게도 저자는 의미론적 분할 네트의 Spatial Pyramid Pooling 블록을 채택하여 다양한 규모의 특징을 결합합니다.
다음으로 저자는 왼쪽 이미지의 특징을 disp 픽셀만큼 수평으로 이동한 오른쪽 이미지의 특징과 연결합니다. 그들은 [0, maxdisparity] 범위의 disp를 사용하고 결과를 4D 볼륨으로 결합합니다.
다음 단계로 3D 컨볼루션 인코더-디코더 아키텍처는 비용 볼륨을 개선하고 개선합니다. 마지막 레이어는 H x W x (최대 디스패리티 + 1) 크기의 기능 맵을 생성하는 3D 컨볼루션입니다.
마지막으로 저자는 soft argmin 함수를 적용하여 불일치를 예측합니다. 출력 H x W x (maxdisparity + 1) 특징 맵의 모든 채널은 서로 다른 디스패리티를 나타냅니다. 저자는 softmax 연산인 \sigma(\cdot)를 사용하여 디스패리티 차원에 걸쳐 확률 볼륨을 정규화합니다. 그들은 확률에 해당하는 가중치와 불일치 d를 결합합니다. 아래 공식은 이 작업을 나타냅니다.
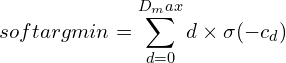
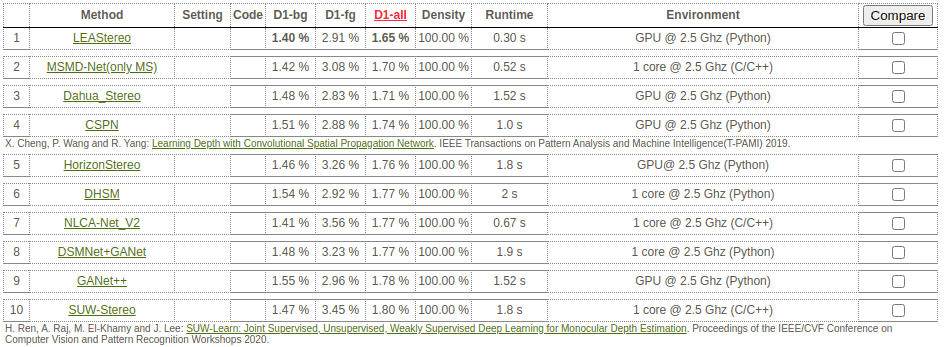
그림 3의 KITTI 벤치마크 결과(2020년 8월 중순)를 보면 상위 스테레오 매칭 접근 방식이 느리다는 것을 알 수 있습니다. KITTI 2015 벤치마크 상위 10위에서 가장 빠른 작업은 GPU를 사용하여 초당 3.3프레임만 제공합니다. 그 이유는 상위 모델이 3D 컨볼루션을 사용하여 품질을 개선하지만 비용은 알고리즘의 속도이기 때문입니다.
상관 레이어를 사용하는 스테레오 매칭 방법(MADNet, DispNetC)이 있지만 3D 컨볼루션 기반 방법에 품질 싸움에서 지고 있습니다.
다른 방법보다 훨씬 빠르면서 최첨단 결과를 얻으려는 최근 접근 방식 중 하나는 AANet입니다.
AANet
일반적인 방법의 아키텍처는 다음과 같습니다.
º 공유 네트워크(특징 추출기)는 왼쪽 및 오른쪽 이미지에서 특징 피라미드를 추출합니다.

에 해당합니다. S는 눈금의 수, s는 눈금 인덱스, s=1은 가장 큰 눈금을 나타냅니다.
º 상관 계층은 다중 규모 3D 비용 볼륨을 구성합니다.

여기서

는 두 특징 벡터의 내적, N은 추출된 특징의 채널 수,

는 해당 위치에서의 매칭 비용 (h, w) 격차 후보 d.
이 상관 계층은 DispNetC의 상관 계층과 유사합니다.
º 여러 적응형 집계 모듈(Adaptive Aggregation Modules)은 비용 볼륨을 집계합니다. 이 모듈은 [GCNet, StereoNet, PSMNet]에서 이전에 사용된 3D 인코더-디코더 네트워크를 대체하며,
º 마지막 단계에서 개선 모듈은 저해상도 디스패리티 예측을 원래 해상도로 업샘플링합니다. AANet은 StereoDRNet에서 제안한 두 가지 개선 모듈을 사용합니다.
아래 그림은 AANet 아키텍처를 보여줍니다.

적응형 집계 모듈(Adaptive Aggregation Module)(AAModule)
이 논문의 주요 참신(major novelty of the paper)인 Adaptive Aggregation Module(AAModule)에 집중해 보겠습니다.
두 가지 주요 부분으로 구성됩니다.
- 규모 내 집계(Intra-Scale Aggregation)(ISA)
- 교차 규모 집계(Cross-Scale Aggregation)(CSA)
규모 내 집계(Intra-Scale Aggregation)
딥 러닝 기반 스테레오 매칭 방법은 일반적으로 창 기반 비용 집계를 수행합니다.

여기서

는 디스패리티 후보 d에 대한 픽셀 p에서의 집계 비용이고, 픽셀 q는 p의 이웃 _N(p)_에 속하고, _w(p, q)_는 집계 가중치, _C( d, q)_는 디스패리티 후보 d에 대한 픽셀 q에서의 원시 매칭 비용입니다.
그러나 디스패리티가 연속적일 때만 잘 작동해야 하지만 객체 경계가 이 가정을 위반합니다.
그렇기 때문에 가중치 함수를 신중하게 설계하고 픽셀이 불일치 불연속성에 미치는 영향을 제거해야 합니다.
이 문제를 edge-fattening 문제라고 합니다.
AANet의 저자는 edge-fattening 문제에 대처하기 위해 간단한 2D 및 3D 컨볼루션에서 사용되는 정규 샘플링 대신 적응 샘플링 방법을 제안합니다. 이 아이디어는 변형 가능한 컨볼루션과 동일합니다.
AANet에 대한 비용 집계 전략은 일반 샘플링 위치에 대한 추가 오프셋을 학습합니다.

여기서

는 샘플링 포인트의 수,

는 k번째 포인트에 대한 집계 가중치,

는 p에 대한 고정 오프셋,

는 학습 가능한 오프셋입니다.
저자는 또한 Deformable ConvNets v2: More Deformable, Better Results의 변조 메커니즘을 사용하여 콘볼루션 가중치를 내용 적응형으로 만듭니다.
최종 비용 집계 공식은 다음과 같습니다.

여기서

는 픽셀 k의 콘텐츠별 가중치입니다.
변형 가능한 컨볼루션과의 유일한 차이점은 그룹의 수입니다. 특징 맵은 G 그룹으로 구성되며 각 채널 그룹에는 고유한 오프셋 _△pk_와 가중치 _m_k_가 있습니다. 원래의 변형 가능한 컨볼루션 구현과는 달리, 특징 맵의 모든 채널이 동일한 오프셋과 가중치를 공유합니다.
교차 규모 집계(Cross-Scale Aggregation)
AANet의 저자는 여러 규모에서 비용 집계를 결합할 것을 제안합니다. 미세한 디테일을 처리하기 위해서는 고해상도에 대한 비용 집계가 필요하며, 거친 해상도에 대한 비용 집계는 텍스처가 낮고 텍스처가 없는 영역에 유리합니다.
AANet은 다음과 같은 방식으로 특징을 결합합니다.

여기서

는 규모 간 비용 집계 후 결과 비용 볼륨,

는 규모 k에서 집계된 비용 볼륨,

는 비용 볼륨을 다른 모양으로 결합하는 함수입니다.
여기의 아이디어는 HRNet의 개념과 동일하며 해당 논문에서 _f_k_를 채택했습니다.

여기서

는 항등 함수이고, stride=2_인 \(s-k)3x3_ 컨볼루션은 피쳐 맵을 _2^{s-k}_번 다운샘플링하는 데 사용되며,

는 쌍선형 업샘플링입니다.
HRNet과의 유일한 차이점은 더 작은 해상도를 가진 특징 맵의 채널 수입니다. HRNet은 일반적으로 특징 추출기가 이러한 방식으로 제공하므로 고해상도 특징 맵보다 저해상도 특징 맵에 더 많은 채널이 있습니다. 대조적으로, AANet은 대규모 특징 맵보다 거친 특징 맵에서 더 적은 채널을 가지고 있습니다. 그 이유는 채널 수가 디스패리티 후보의 수를 나타내므로 대략적인 표현은 디스패리티 수준이 더 적기 때문입니다.
결과
저자는 제안된 모듈의 중요성을 증명하기 위해 절제 연구를 수행합니다. AANet에서 ISA 및 CSA 모듈을 제거하면 품질이 저하됩니다.

그들은 또한 3D 컨볼루션 인코더-디코더를 ISA 및 CSA 모듈로 대체하여 몇 가지 인기 있는 접근 방식으로 대체했으며 상당한 속도 향상과 메모리 소비 감소를 달성했습니다.
그 이상으로 StereoNet, GCNet 및 PSMNet의 품질이 향상됩니다. GANet의 경우 무시할 수 있는 품질 저하만 있습니다.
저자는 AA 접미사가 있는 수정된 아키텍처를 나타냅니다.

저자는 변형 가능한 컨볼루션이 있는 hourglass networks로 GANet-AA의 개선 모듈을 수정하고 결과 모델을 AANet+라고 부릅니다.
그들은 AANet 및 AANet+를 SceneFlow(그림 7) 및 KITTI(그림 8) 데이터 세트의 해당 데이터와 비교합니다.


저자는 SceneFlow 및 KITTI 데이터 세트로 모델을 훈련했습니다. 그러나 신경망은 다른 영역에서 좋은 결과를 보여줍니다. 예를 들어 그림 10에서 Middlebury 데이터 세트의 샘플에 대한 결과를 볼 수 있습니다.


Code
작성자는 리포지토리에서 교육, 평가 및 추론을 위한 코드를 제공합니다.
'영상처리 > 스테레오 비전' 카테고리의 다른 글
| stereo camera - circle (0) | 2023.05.06 |
|---|---|
| 스테레오 카메라와 YOLOv8을 사용한 거리 추정 (0) | 2023.04.10 |
| 렌즈 왜곡 이해하기 (0) | 2023.04.10 |
| 이미지 형성의 기하학 (0) | 2023.04.10 |
| OpenCV를 사용한 카메라 보정 (0) | 2023.04.10 |


