에피폴라 기하학 및 스테레오 비전 소개
https://learnopencv.com/introduction-to-epipolar-geometry-and-stereo-vision/
Introduction to Epipolar Geometry and Stereo Vision | LearnOpenCV #
We will learn the concepts of Epipolar geometry and point correspondences. We will then use these concepts discuss how to calculate depth from stereo disparity.
learnopencv.com
위의 글을 구글 번역기로 돌린 결과물
에피폴라 기하학 및 스테레오 비전 소개
그 특별한 3D 안경을 쓰고 영화를 볼 때 왜 그 놀라운 3D 효과를 경험할 수 있는지 궁금해 한 적이 있습니까? 아니면 한쪽 눈을 감고 크리켓 공을 잡기가 어려운 이유는 무엇입니까? 이 모든 것은 두 눈을 사용하여 깊이를 인식하는 능력인 입체시와 관련이 있습니다. 이 게시물은 OpenCV 및 스테레오 비전을 사용하여 컴퓨터에 깊이를 인식하는 능력을 제공합니다. 코드는 Python 및 C++로 제공됩니다.

위 GIF의 멋진 부분은 다른 물체를 감지하는 것 외에도 컴퓨터가 물체의 거리를 알 수 있다는 것입니다. 즉, 깊이를 감지할 수 있습니다! 이 비디오에서는 OAK-D(OpenCV AI Kit-Gepth)의 스테레오 카메라 설정을 사용하여 컴퓨터가 깊이를 인식할 수 있도록 했습니다.
스테레오 카메라 설정이란 무엇입니까? 컴퓨터에 깊이감을 제공하기 위해 어떻게 사용합니까? 입체시와 관련이 있습니까?
이 게시물은 에피폴라 기하학 및 스테레오 비전과 관련된 기본 개념을 이해하여 이러한 질문에 답하려고 합니다.
포스트의 이론적인 설명은 대부분 Richard Hartley와 Andrew Zisserman의 책: 컴퓨터 비전의 다중 보기 기하학에서 영감을 받았습니다. 컴퓨터 비전의 다양한 기본 개념을 이해하기 위한 매우 유명하고 표준적인 교과서입니다.
이 게시물은 공간 AI 소개 시리즈(Introduction to Spatial AI series)의 첫 번째 부분입니다. 다양한 기본 개념에 대한 자세한 소개를 제공하고 시리즈의 후속 부분에 대한 강력한 기반을 만듭니다.
엄청난! 이제 시작하여 컴퓨터가 깊이를 인식하도록 돕습니다!
깊이를 계산하기 위해 하나 이상의 이미지가 필요합니까?
이미지에서 3D 개체를 캡처(투영)할 때 3D 공간에서 2D(평면) 투영 공간으로 투영합니다. 이것을 평면 투영이라고 합니다. 문제는 이 평면 투영으로 인해 깊이 정보를 잃는다는 것입니다.
그렇다면 깊이를 어떻게 회복할까요? 단일 이미지를 사용하여 장면의 깊이를 다시 계산할 수 있습니까? 간단한 예를 들어 보겠습니다.

그림 1에서 C1과 X는 3D 공간의 점이고 단위 벡터 L1은 C1에서 X까지의 광선 방향을 나타냅니다. 이제 점 C1과 방향 벡터 L1의 값을 알면 X를 찾을 수 있습니까? 수학적으로는 단순히 방정식에서 X를 푸는 것을 의미합니다.

이제 k의 값을 알 수 없으므로 X의 고유한 값을 찾을 수 없습니다.

그림 2에서 추가 점 C2가 있고 L2는 C2에서 X를 통과하는 광선의 방향 벡터입니다. 이제 C2와 L2도 알고 있는 경우 X에 대한 고유한 값을 찾을 수 있습니까?
예! C1과 C2에서 발생하는 광선은 고유한 점에서 분명히 교차하므로 점 X 자체입니다. 이것을 삼각측량(triangulation)이라고 합니다. 우리는 점 X를 삼각 측량했다고 말합니다.

그림 3은 두 개의 다른 보기(이미지)에서 캡처(투영)할 때 점(X)의 깊이를 계산하기 위해 삼각 측량을 사용하는 방법을 보여줍니다. 이 그림에서 C1과 C2는 각각 왼쪽과 오른쪽 카메라의 알려진 3D 위치입니다. x1은 왼쪽 카메라가 촬영한 3D 점 X의 이미지이고 x2는 오른쪽 카메라가 촬영한 X의 이미지입니다. x1과 x2는 동일한 3D 점의 투영이기 때문에 대응 점이라고 합니다. x1과 C1을 사용하여 L1을 찾고 x2와 C2를 사용하여 L2를 찾습니다. 따라서 그림 2에서와 같이 삼각분할을 사용하여 X를 찾을 수 있습니다.
위의 예에서 서로 다른 보기에서 캡처하는 두 개의 이미지를 사용하여 3D 점을 삼각 측량하려면 주요 요구 사항이 다음과 같다는 것을 배웠습니다.
- 카메라 위치(Position of the cameras) – C1 및 C2.
- 포인트 대응(Point correspondence) – x1 및 x2.
엄청난! 이제 깊이를 찾기 위해 하나 이상의 이미지가 필요하다는 것이 분명해졌습니다.
여기요! 그러나 이것은 우리가 계산하려고 한 단일 3D 점에 불과했습니다. 두 개의 다른 보기에서 캡처하여 실제 장면의 3D 구조를 계산하는 방법은 무엇입니까? 분명한 대답은 두 뷰에서 캡처된 모든 3D 포인트에 대해 위의 프로세스를 반복하는 것입니다. 이를 수행하는 데 있어 실제적인 문제를 자세히 살펴보겠습니다. 현실 확인 시간!
Two-View 기하학에 대한 실용적이고 이론적인 이해

그림 4는 서로 다른 관점에서 실제 장면을 캡처한 두 개의 이미지를 보여줍니다. 3D 구조를 계산하기 위해 앞에서 언급한 두 가지 핵심 요구 사항을 찾으려고 합니다.
- 실제 좌표계(C1 및 C2)에서 카메라의 위치. 카메라 위치(C1 또는 C2) 중 하나를 원점으로 가정하여 3D 점을 계산하여 이 문제를 단순화합니다. 알려진 보정 패턴을 사용하여 두 개의 보기 시스템을 보정하여 이를 찾습니다. 이 프로세스를 스테레오 보정(stereo calibration)이라고 합니다.
- 계산할 장면의 각 3D 포인트(X)에 대한 포인트 대응(x1 및 x2)입니다. 포인트 대응 계산을 위한 다양한 개선 사항에 대해 논의하고 마지막으로 에피폴라 기하학이 문제를 단순화하는 데 어떻게 도움이 되는지 이해할 것입니다.
스테레오 카메라 보정은 서로에 대해 단단히 고정된 한 쌍의 카메라로 이미지를 캡처하는 경우에만 유용합니다. 한 대의 카메라가 두 개의 다른 각도에서 이미지를 캡처한다면 우리는 규모만큼만 깊이를 찾을 수 있습니다. 실제 스케일을 찾는 데 사용할 수 있는 캡처된 장면에 대한 특별한 기하학적 정보가 없으면 절대 깊이를 알 수 없습니다.

그림 5는 수동으로 표시된 서로 다른 일치 지점을 보여줍니다. 해당 지점을 식별하는 것은 쉽지만 컴퓨터가 그렇게 하도록 하려면 어떻게 해야 합니까?
사람들이 컴퓨터 비전 커뮤니티에서 일반적으로 사용하는 한 가지 방법을 특성 매칭(feature matching)라고 합니다. 다음 그림 6은 ORB 특성 설명자(ORB feature descriptors)를 사용하여 왼쪽과 오른쪽 이미지 간의 일치된 특성을 보여줍니다. 이것은 포인트 대응(일치)을 찾는 한 가지 방법입니다.

그러나 총 픽셀 수에 대한 알려진 포인트 대응 픽셀 수의 비율이 최소임을 관찰합니다. 이것은 우리가 매우 드물게 재구성된 3D 장면(sparsely reconstructed 3D scene)을 갖게 된다는 것을 의미합니다. 조밀한 재구성을 위해서는 가능한 최대 픽셀 수에 대한 포인트 대응을 얻어야 합니다.

그림 7 - 템플릿 매칭을 사용한 다중 매칭 포인트. 포인트 대응을 찾는 간단한 방법은 유사한 인접 픽셀 정보를 가진 픽셀을 찾는 것입니다. 그림 7에서 유사한 인접 정보를 가진 픽셀을 일치시키는 이 방법을 사용하면 한 이미지의 단일 픽셀이 다른 이미지에서 여러 일치를 갖는 결과를 얻습니다. 우리는 진정한 일치를 결정하는 알고리즘을 작성하는 것이 어렵다는 것을 알게 되었습니다.
검색 공간을 줄이는 방법이 있습니까? 부정확한 대응으로 이어지는 모든 추가 잘못된 일치를 제거하는 데 사용할 수 있는 몇 가지 정리(theorem)는 무엇입니까? 여기에서 에피폴라 기하학을 사용합니다.
이 모든 설명과 빌드업은 에피폴라 기하학(epipolar geometry)의 개념을 소개하기 위한 것이었습니다. 이제 우리는 점 대응(point correspondence)을 위한 검색 공간을 줄이는 데 있어 에피폴라 기하학의 중요성을 이해할 것입니다.
에피폴라 기하학과 점 대응에서의 사용

그림 8에서 그림 3과 유사한 설정을 가정합니다. 3D 점 X는 각각 C1 및 C2의 카메라에 의해 x1 및 x2에서 캡처됩니다. x1은 X의 투영이므로 x1을 통과하는 C1에서 광선 R1을 확장하려고 하면 X도 통과해야 합니다. 이 광선 R1은 라인 L2로 캡처되고 X는 이미지 i2에서 x2로 캡처됩니다. X가 R1에 있는 것처럼 x2는 L2에 있어야 합니다. 이런 식으로 x2의 가능한 위치는 한 줄로 제한되므로 픽셀 x1에 해당하는 이미지 i2의 픽셀에 대한 검색 공간이 한 줄 L2로 축소된다고 말할 수 있습니다. L2를 찾기 위해 에피폴라 기하학을 사용합니다.
이제 몇 가지 기술 용어를 정의할 시간입니다! X와 함께 각각의 반대 이미지에 카메라 중심을 투영할 수도 있습니다. e2는 이미지 i2의 카메라 중심 C1의 투영이고 e1은 이미지 i1의 카메라 중심 C2의 투영입니다. e1 및 e2의 기술 용어는 에피폴입니다. 따라서 2-뷰 지오메트리 설정(two-view geometry setup)에서 에피폴은 다른 뷰에서 한 뷰의 카메라 중심 이미지입니다.
두 카메라 중심을 연결하는 선을 기준선이라고 합니다. 따라서 에피폴은 기준선과 이미지 평면의 교차로 정의할 수도 있습니다.
그림 8은 R1과 기준선을 사용하여 평면 P를 정의할 수 있음을 보여줍니다. 이 평면에는 X, C1, x1, x2 및 C2도 포함됩니다. 우리는 이 평면을 에피폴라 평면이라고 부릅니다. 또한, 에피폴라 평면과 이미지 평면이 교차하는 선을 에피폴라 라인이라고 합니다. 따라서 이 예에서 L2는 에피폴라 라인입니다. 다른 X 값에 대해 서로 다른 에피폴라 평면과 서로 다른 에피폴라 라인을 갖게 됩니다. 그러나 모든 에피폴라 평면은 기준선에서 교차하고 모든 에피폴라 선은 에피폴에서 교차합니다. 이 모든 것이 함께 에피폴라 기하학을 형성합니다.
우리가 지금까지 배운 모든 기술 용어로 그림 8을 다시 방문하십시오.
베이스라인 B와 광선 R1을 사용하여 생성된 에피폴라 평면 P가 있습니다. e1과 e2는 에피폴이고 L2는 에피폴라 라인입니다. 주어진 그림의 에피폴라 기하학에 기초하여, 픽셀 x1에 대응하는 이미지 i2의 픽셀에 대한 검색 공간은 에피폴라 라인 L2인 단일 2D 라인으로 제한됩니다. 이것을 에피폴라 제약이라고 합니다.
단일 행렬로 전체 에피폴라 기하학을 표현하는 방법이 있습니까? 또한 두 개의 캡처된 이미지만 사용하여 이 행렬을 계산할 수 있습니까? 좋은 소식은 그러한 행렬이 있다는 것인데, 이를 기본 행렬이라고 합니다.
다음 두 섹션에서는 먼저 투영 기하학(projective geometry)과 동종 표현(homogeneous representation)이 의미하는 바를 이해한 다음 기본 행렬 표현을 유도하려고 합니다. 마지막으로 기본 행렬을 사용하여 에피폴라 라인을 계산하고 에피폴라 제약 조건을 나타냅니다.
투영 기하학(projective geometry) 및 동종 표현(homogeneous representation)의 이해
2D 평면에서 선을 어떻게 표현합니까? 2D 평면에서 선의 방정식은 ax + by + c = 0입니다. a, b, c의 다른 값으로 2D 평면에서 다른 선을 얻습니다. 따라서 벡터(a,b,c)를 사용하여 선을 나타낼 수 있습니다.
라인 ln1이 2x + 3y + 7 = 0으로 정의되고 라인 ln2가 4x + 6y + 14 = 0으로 정의된다고 가정합니다. 위의 논의에 따라 l1은 벡터 (2,3,7)로, l2는 벡터 (4,6,14)과 같이 나타낼 수 있습니다. l1과 l2는 본질적으로 같은 선을 나타내고 벡터(4,6,14)는 기본적으로 벡터(2,3,7)의 크기가 2배만큼 크기가 조정된 버전이라고 쉽게 말할 수 있습니다.
따라서 두 벡터(a,b,c)와 k(a,b,c)(여기서 k는 0이 아닌 스케일링 상수)는 동일한 선을 나타냅니다. 스케일링 상수만으로 관련된 이러한 등가(equivalent) 벡터는 동종 벡터(homogeneous vectors)의 클래스를 형성합니다. 벡터 (a,b,c)는 각각의 등가 벡터 클래스의 동종 표현(homogeneous representation)입니다.
a=b=c=0 이외의 가능한 모든 실수 값 a,b,c에 대해 (a,b,c)로 표시되는 모든 등가 클래스의 집합은 투영 공간(projective space)을 형성합니다. 우리는 투영 공간(projective space)에서 점, 선, 평면 등과 같은 요소를 정의하기 위해 동종 좌표(homogeneous coordinates)의 동종 표현(homogeneous representation)을 사용합니다. 우리는 투영 기하학(projective geometry)의 규칙을 사용하여 투영 공간에서 이러한 요소에 대한 변환을 수행합니다.
기본 행렬(Fundamental matrix) 유도
그림 3에서 두 카메라의 카메라 투영 행렬(projection matrices)을 알고 있다고 가정합니다. 예를 들어 C1에 있는 카메라의 경우 P1, C2에 있는 카메라의 경우 P2입니다.
투영 행렬(projection matrix)이란 무엇입니까? 카메라의 투영 행렬은 3D 세계 좌표와 카메라에 캡처된 해당 픽셀 좌표 간의 관계를 정의합니다. 카메라 투영 행렬에 대해 자세히 알아보려면 카메라 보정에 대한 이 게시물을 읽으십시오.
P1이 3D 세계 좌표를 이미지 좌표로 투영하는 것처럼 P1의 의사 역인 P1inv를 정의하여 x1과 X를 통과하는 C1의 광선 R1을 다음과 같이 정의할 수 있습니다.

k는 C1에서 X까지의 실제 거리를 모르기 때문에 스케일링 매개변수입니다. Ln2가 i2에서 캡처된 광선 R1의 이미지라는 것을 알고 있으므로 i1의 픽셀 x1에 해당하는 i2의 픽셀에 대한 검색 공간을 줄이기 위해 에피폴라 라인 Ln2를 찾아야 합니다. 따라서 Ln2를 계산하려면 먼저 광선 R1에서 두 점을 찾고 P2를 사용하여 이미지 i2에 투영하고 두 점의 투영된 이미지를 사용하여 Ln2를 찾습니다.
R1에서 고려할 수 있는 첫 번째 점은 광선이 이 점에서 시작하기 때문에 C1입니다. 두 번째 점은 k=0을 유지하여 계산할 수 있습니다. 따라서 우리는 점을 C1 및 (P1inv)(x1)로 얻습니다.
투영 행렬 P2를 사용하여 이미지 i2에서 이러한 점의 이미지 좌표를 각각 P2*C1 및 P2*P1inv*x1로 얻습니다. 우리는 또한 P2*C1이 기본적으로 이미지 i2에서 에피폴 e2임을 관찰합니다.
선은 단순히 외적 p1 x p2를 찾아 두 점 p1과 p2를 사용하는 투영 기하학에서 정의할 수 있습니다. 따라서
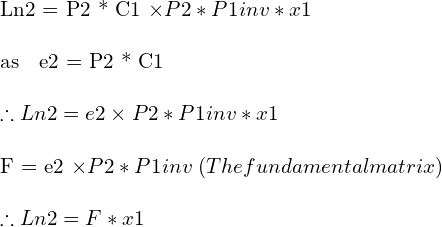
투영 기하학에서 점 x가 선 L에 있으면 방정식의 형태로 쓸 수 있습니다.
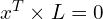
따라서 x2가 에피폴라 라인 Ln2에 있으므로 다음을 얻습니다.

위의 방정식에서 Ln2의 값을 대체하여 다음 방정식을 얻습니다.

이것은 두 점 x1, x2가 대응점이 되기 위한 필요조건이며, 에피폴라 제약의 한 형태이기도 하다. 따라서 F는 2-뷰 시스템의 전체 에피폴라 기하학을 나타냅니다.
이 방정식의 또 다른 특별한 점은 무엇입니까? 그것은 에피폴라 라인을 찾는 데 사용할 수 있습니다!
기본 행렬을 사용하여 에피폴라 라인 찾기
x1과 x2는 방정식에서 대응하는 점이므로 ORB 또는 SIFT와 같은 특성 일치 방법을 사용하여 일부 점에 대한 대응을 찾을 수 있으면 F에 대한 위의 방정식을 푸는 데 사용할 수 있습니다.
OpenCV의 findFundamentalMat() 메서드는 7-포인트 알고리즘, 8-포인트 알고리즘, RANSAC 알고리즘 및 LMedS 알고리즘과 같은 다양한 알고리즘의 구현을 제공하여 일치하는 특징점을 사용하여 기본 행렬을 계산합니다.
F가 알려지면 공식을 사용하여 에피폴라 라인 Ln2를 찾을 수 있습니다.
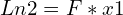
Ln2를 알면 에피폴라 제약 조건을 사용하여 픽셀 x1에 해당하는 픽셀 x2에 대한 검색을 제한할 수 있습니다.
Two-View Vision의 특별한 경우 – 평행 이미징 평면
우리는 대응 문제(correspondence problem)를 해결하기 위해 노력해 왔습니다. 우리는 특성 매칭을 사용하여 시작했지만 전체 픽셀의 작은 부분에 대한 포인트 대응이 알려져 있기 때문에 희소 3D 구조(sparse 3D structure)로 이어지는 것을 관찰했습니다. 그런 다음 픽셀 대응을 위해 템플릿 기반 검색을 사용하는 방법을 보았습니다. 우리는 에피폴라 기하학을 사용하여 포인트 대응을 위한 검색 공간을 단일 라인인 에피폴라 라인으로 줄이는 방법을 배웠습니다.
조밀한 점 대응을 찾는 이 프로세스를 더 단순화할 수 있습니까?


그림 9와 그림 10은 서로 다른 두 쌍의 이미지에 대한 특성 매칭 결과와 에피폴라 라인 제약(epipolar line constraint)을 보여줍니다. 특성 매칭과 에피폴라 라인 측면에서 두 그림의 가장 중요한 차이점은 무엇입니까?
예! 당신이 옳았다! 그림 10에서 일치하는 특성점의 수직 좌표는 동일합니다. 해당하는 모든 점의 수직 좌표는 동일합니다. 그림 10의 모든 에피폴라 라인은 평행해야 하며 왼쪽 이미지의 각 지점과 동일한 수직 좌표를 가져야 합니다. 글쎄요, 그게 뭐가 그렇게 대단해요?
정확히! 그림 9의 경우와 달리 각 에피폴라 라인을 명시적으로 계산할 필요가 없습니다. 왼쪽 이미지의 픽셀이 (x1,y1)에 있는 경우 두 번째 이미지의 각 에피폴라 라인의 방정식은 y=y1입니다.
오른쪽 이미지의 같은 행에 있는 해당 픽셀에 대해 왼쪽 이미지의 각 픽셀을 검색합니다. 이것은 이미징 평면이 평행한 2-뷰 기하학의 특별한 경우입니다. 따라서 에피폴(다른 카메라가 포착한 한 카메라의 이미지)은 무한대에서 형성됩니다. 에피폴라 기하학에 대한 이해를 바탕으로 에피폴라 라인은 에피폴에서 만납니다. 따라서 이 경우 에피폴이 무한대에 있으므로 에피폴라 선은 평행합니다.
대박! 이것은 조밀한 점 대응(dense point correspondence) 문제를 상당히 단순화합니다. 그러나 여전히 각 점에 대해 삼각 측량을 수행해야 합니다. 이 문제도 단순화할 수 있습니까? 음, 다시 한 번 평행 이미징 평면의 특별한 경우는 우리에게 희소식입니다! 스테레오 시차(stereo disparity)를 적용하는 데 도움이 됩니다. 입체시(stereopsis)나 입체시(stereoscopic vision)와 유사하며 인간이 깊이를 인지하도록 돕는 방식이다. 이것을 자세히 이해합시다.
스테레오 시차(stereo disparity) 이해
다음 gif는 Middlebury Stereo Datasets 2005의 이미지를 사용하여 생성되었습니다. 이는 이미지 평면을 평행하게 만드는 카메라의 순수한 변환 동작을 보여줍니다. 어떤 물체가 카메라에 더 가까이 있는지 알 수 있습니까?

맨 아래에 있는 소 장난감이 맨 위 줄에 있는 장난감보다 카메라에 더 가깝다고 분명히 말할 수 있습니다. 우리는 이것을 어떻게 했는가? 우리는 기본적으로 두 이미지에서 물체의 이동을 봅니다. 이동이 가까울수록 개체입니다. 이러한 변화를 우리는 시차(disparity)라고 부릅니다.
깊이 계산을 위한 점 삼각 측량(point triangulation)을 피하기 위해 어떻게 사용합니까? 각 픽셀에 대한 시차(두 이미지의 픽셀 이동)를 계산하고 비례 매핑을 적용하여 주어진 시차 값에 대한 깊이를 찾습니다. 이것은 그림 12에서 더 정당화됩니다.
Image explaining the relationship between disparity and depth map
그림 12. 시차(x – x')와 깊이 Z 간의 관계를 설명하는 OpenCV 문서의 이미지.
Disparity = x – x’ = Bf/Z
여기서 B는 기준선(카메라 간 거리)이고 f는 초점 거리입니다.
OpenCV의 StereoSGBM 방법을 사용하여 주어진 이미지 쌍에 대한 디스패리티 맵을 계산하는 코드를 작성합니다. StereoSGBM 방법은 [3]을 기반으로 합니다.
C++
// Reading the left and right images.
cv::Mat imgL,imgR;
imgL = cv::imread("../im0.png"); // path to left image is "../im0.png"
imgR = cv::imread("../im1.png"); // path to left image is "../im1.png"
// Setting parameters for StereoSGBM algorithm
int minDisparity = 0;
int numDisparities = 64;
int blockSize = 8;
int disp12MaxDiff = 1;
int uniquenessRatio = 10;
int speckleWindowSize = 10;
int speckleRange = 8;
// Creating an object of StereoSGBM algorithm
cv::Ptr<cv::StereoSGBM> stereo = cv::StereoSGBM::create(minDisparity,numDisparities,blockSize,
disp12MaxDiff,uniquenessRatio,speckleWindowSize,speckleRange);
// Calculating disparith using the StereoSGBM algorithm
cv::Mat disp;
stereo->compute(imgL,imgR,disp);
// Normalizing the disparity map for better visualisation
cv::normalize(disp, disp, 0, 255, cv::NORM_MINMAX, CV_8UC1);
// Displaying the disparity map
cv::imshow("disparity",disp);
cv::waitKey(0);
Python
# Reading the left and right images.
imgL = cv2.imread("../im0.png",0)
imgR = cv2.imread("../im1.png",0)
# Setting parameters for StereoSGBM algorithm
minDisparity = 0;
numDisparities = 64;
blockSize = 8;
disp12MaxDiff = 1;
uniquenessRatio = 10;
speckleWindowSize = 10;
speckleRange = 8;
# Creating an object of StereoSGBM algorithm
stereo = cv2.StereoSGBM_create(minDisparity = minDisparity,
numDisparities = numDisparities,
blockSize = blockSize,
disp12MaxDiff = disp12MaxDiff,
uniquenessRatio = uniquenessRatio,
speckleWindowSize = speckleWindowSize,
speckleRange = speckleRange
)
# Calculating disparith using the StereoSGBM algorithm
disp = stereo.compute(imgL, imgR).astype(np.float32)
disp = cv2.normalize(disp,0,255,cv2.NORM_MINMAX)
# Displaying the disparity map
cv2.imshow("disparity",disp)
cv2.waitKey(0)
다른 매개변수를 사용하여 최종 출력 디스패리티 맵 계산에 미치는 영향을 관찰해 보십시오. StereoSGBM에 대한 자세한 설명은 이후의 Introduction to Spatial AI 시리즈에서 제공될 예정입니다. 다음 게시물에서는 자체 스테레오 카메라 설정을 만들고 라이브 시차 맵 비디오를 녹화하는 방법을 배우고 시차 맵을 깊이 맵으로 변환하는 방법도 배웁니다. 스테레오 카메라의 흥미로운 응용 프로그램도 설명할 예정이지만 지금으로서는 놀랍습니다!
참고문헌
[1] Richard Hartley와 Andrew Zisserman. 2003. 컴퓨터 비전의 다중 보기 기하학(2nd. ed.). 케임브리지 대학 출판부, 미국.
[2] D. Scharstein, H. Hirschmüller, Y. Kitajima, G. Krathwohl, N. Nesic, X. Wang 및 P. Westling. 서브픽셀 단위의 정확한 실측이 포함된 고해상도 스테레오 데이터세트. 2014년 9월 독일 뮌스터에서 열린 패턴 인식에 관한 독일 회의(GCPR 2014)에서.
[3] H. Hirschmuller, "Semiglobal Matching and Mutual Information에 의한 스테레오 처리", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 30, 아니. 2, pp. 328-341, 2008년 2월, doi: 10.1109/TPAMI.2007.1166.