렌즈 왜곡 이해하기
https://learnopencv.com/understanding-lens-distortion/
Understanding Lens Distortion | LearnOpenCV #
In a previous post, we went over the geometry of image formation and learned how a point in 3D gets projected on to the image plane of a camera. The model we used was based on the pinhole camera model. The only time you use a pinhole camera is probably dur
learnopencv.com
위 글을 구글 번역기로 돌린 결과물
렌즈 왜곡 이해하기
이전 게시물에서 이미지 형성의 기하학을 살펴보고 3D의 한 점이 카메라의 이미지 평면에 투영되는 방법을 배웠습니다.
우리가 사용한 모델은 핀홀 카메라 모델을 기반으로 했습니다. 핀홀 카메라를 사용하는 유일한 시간은 아마도 일식 동안일 것입니다.
모든 실제 카메라의 이미지 형성 모델에는 렌즈가 포함됩니다.
왜 우리가 카메라에 렌즈를 부착하는지 궁금하신가요? 이미지의 해당 픽셀에 대한 3D 포인트의 투영을 정의하는 변환에 영향을 줍니까? 그렇다면 수학적으로 어떻게 모델링합니까?
이 포스트에서 우리는 위의 질문에 답할 것입니다.
핀홀을 렌즈로 교체
선명하고 선명한(clear and sharp) 이미지를 생성하려면 핀홀 카메라의 조리개(구멍) 직경이 가능한 작아야 합니다. 조리개의 크기를 늘리면 물체의 여러 지점에서 나오는 광선이 화면의 동일한 부분에 입사되어 흐린 이미지를 생성한다는 것을 알 수 있습니다.
반면에 조리개 크기를 작게 만들면 적은 수의 광자만 이미지 센서에 닿습니다. 결과적으로 이미지가 어둡고 시끄럽습니다(dark and noisy).
따라서 핀홀 카메라의 조리개가 작을수록 이미지에 초점이 맞춰지지만 동시에 더 어둡고 시끄럽습니다(darker and noisier).
반면에 조리개가 클수록 이미지 센서는 더 많은 광자를 수신합니다(따라서 더 많은 신호). 이것은 적은 양의 노이즈로 밝은 이미지로 이어집니다.
선명한 이미지를 얻는 동시에 이미지를 밝게 만들기 위해 더 많은 광선을 캡처하는 방법은 무엇입니까?
우리는 핀홀을 렌즈로 대체하여 광선이 통과할 수 있는 조리개의 크기를 늘립니다. 렌즈를 사용하면 더 많은 수의 광선이 구멍을 통과할 수 있으며 광학적 특성으로 인해 화면에 초점을 맞출 수도 있습니다. 이것은 이미지를 더 밝게 만듭니다.
대박! 그래서 우리는 렌즈를 사용하여 밝고 선명하고 초점이 맞는 이미지를 가지고 있습니다.
문제가 해결되었습니까? 맞지? 그렇게 빠르지 않습니다. 공짜는 없다!
왜곡 효과의 주요 유형 및 원인
렌즈를 사용하면 더 나은 품질의 이미지를 얻을 수 있지만 렌즈에는 약간의 왜곡 효과가 있습니다. 왜곡 효과에는 두 가지 주요 유형이 있습니다.
- 방사형 왜곡(Radial distortion): 이러한 유형의 왜곡은 일반적으로 빛의 불균등한 굽힘으로 인해 발생합니다. 광선은 렌즈 중앙 근처의 광선보다 렌즈 가장자리 근처에서 더 많이 구부러집니다. 방사형 왜곡으로 인해 실제 세계의 직선은 이미지에서 곡선으로 나타납니다. 광선은 이미지 센서에 닿기 전에 이상적인 위치에서 방사상으로 안쪽 또는 바깥쪽으로 변위됩니다. 방사형 왜곡 효과에는 두 가지 유형이 있습니다.
1. 음의 방사상 변위에 해당하는 배럴 왜곡(Barrel distortion) 효과
2. 양의 방사상 변위에 해당하는 핀쿠션 왜곡(Pincushion distortion) 효과. - 접선 왜곡(Tangential distortion): 일반적으로 이미지 화면이나 센서가 렌즈와 비스듬한 각도에 있을 때 발생합니다. 따라서 이미지가 기울어지고 늘어진 것처럼 보입니다.

[1]에 따르면 왜곡의 원인에 따라 방사형 왜곡, 편심 왜곡 및 얇은 프리즘 왜곡(radial distortion, decentering distortion and thin prism distortion)의 3가지 유형이 있습니다. 편심 및 얇은 프리즘 왜곡에는 방사형 및 접선 왜곡(radial and tangential distortion) 효과가 있습니다.

이제 렌즈에 의해 어떤 유형의 왜곡 효과가 발생하는지 더 잘 알 수 있습니다. 하지만 왜곡된 이미지는 어떻게 보이나요? 렌즈에 의해 발생하는 왜곡에 대해 걱정할 필요가 있습니까? 그렇다면 왜? 어떻게 처리합니까?

위의 그림은 렌즈가 가져올 수 있는 왜곡 효과의 예입니다. 그림 3을 그림 1과 연관시키면 방사형 왜곡 효과의 일종인 배럴 왜곡 효과라고 할 수 있습니다. 이제 오른쪽 문의 높이를 구하라는 요청을 받았다면 어떤 두 가지 점을 고려하시겠습니까? SLAM을 수행하거나 이미지에 높은 왜곡 효과가 있는 카메라로 일부 증강 현실 응용 프로그램을 만들 때는 상황이 훨씬 더 어려워집니다.
렌즈 왜곡을 수학적으로 표현하기
이미지에서 현실 세계의 3D 점을 추정하려고 할 때 이러한 왜곡 효과를 고려해야 합니다.
렌즈 속성을 기반으로 왜곡 효과를 수학적으로 모델링하고 이 시리즈의 이전 게시물에서 설명한 핀홀 카메라 모델과 결합합니다. 따라서 이전 게시물에서 논의한 고유 및 외부 매개변수와 함께 추가 고유 매개변수로 왜곡 계수(수학적으로 렌즈 왜곡을 나타냄)도 있습니다.
카메라 모델에서 이러한 왜곡을 고려하기 위해 핀홀 카메라 모델을 다음과 같이 수정합니다.
(1)

(2)

(3)

(4)
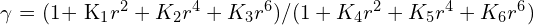
(5)

(6)

(7)

(8)

calibreteCamera 메서드에서 반환된 distCoeffs 행렬은 방사형 왜곡을 나타내는 K_1 ~ K_6 값과 접선 왜곡을 나타내는 P_1 , P_2 값을 제공합니다. 렌즈 왜곡을 나타내는 위의 수학적 모델에는 모든 유형의 왜곡, 방사형 왜곡, 편심 왜곡 및 얇은 프리즘 왜곡(radial distortion, decentering distortion and thin prism distortion)이 포함되므로 계수 K_1 ~ K_6은 순 방사형 왜곡을 나타내고 P_1 및 P_2는 순 접선 왜곡을 나타냅니다.
엄청난 ! 따라서 카메라 보정에 대한 이 시리즈의 게시물에서는 이미지 형성의 기하학으로 시작한 다음 카메라 보정을 수행하고 관련된 기본 이론에 대해 논의했으며 핀홀 카메라의 수학적 모델에 대해서도 논의했으며 마지막으로 이 게시물에서 렌즈 왜곡에 대해 논의했습니다. 이러한 이해를 바탕으로 이제 자신만의 가상 카메라를 만들고 OpenCV 및 Numpy를 사용하여 몇 가지 흥미로운 효과를 시뮬레이션할 수 있습니다. Numpy 계산만 사용하여 가상 카메라가 구현된 이 저장소를 참조할 수 있습니다. 고유 및 외부 매개변수를 모두 사용하면 카메라의 각 매개변수가 최종 이미지에 미치는 영향을 더 잘 느낄 수 있습니다.
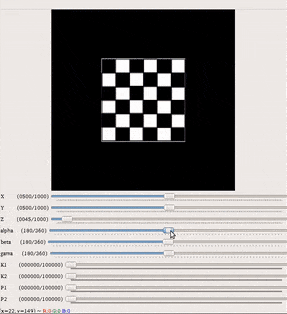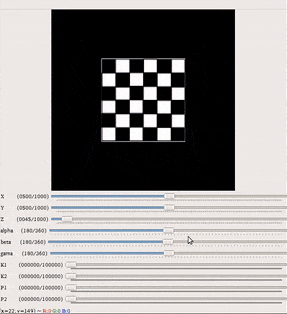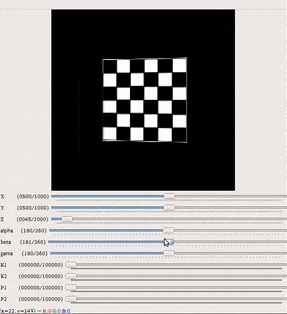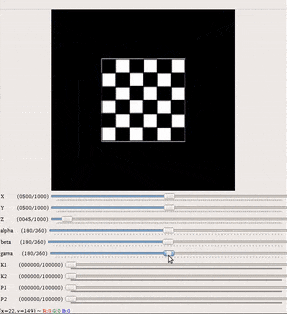

가상 카메라 시뮬레이션을 사용하여 회전 효과(윗쪽), 외부 매개변수 및 겉보기 픽셀 크기의 영향(아랫쪽), 내부 매개변수를 보여주는 GIF.
저장소에 제공된 GUI를 사용하여 변경할 수 있는 몇 가지 다른 매개변수가 있습니다. 다양한 카메라 매개변수의 효과에 대해 더 나은 직관을 갖는 데 도움이 됩니다.
OpenCV를 사용하여 왜곡 제거
그러면 교정 단계 후에 무엇을 합니까? 카메라 보정에 대한 이전 게시물에서 카메라 매트릭스와 왜곡 계수를 얻었지만 값을 어떻게 사용합니까?
한 가지 응용 프로그램은 파생된 왜곡 계수를 사용하여 이미지를 왜곡하지 않는 것입니다. 아래에 표시된 이미지는 렌즈 왜곡의 영향과 카메라 보정에서 얻은 계수에서 제거하는 방법을 보여줍니다.

렌즈로 인한 왜곡을 제거하는 세 가지 주요 단계가 있습니다.
- 카메라 보정을 수행하고 고유한 카메라 매개변수를 가져옵니다. 이것은 이 시리즈의 이전 게시물에서 수행한 작업입니다. 고유 매개변수에는 카메라 왜곡 매개변수도 포함됩니다.
- 왜곡되지 않은 이미지에서 원하지 않는 픽셀의 비율을 제어하기 위해 카메라 매트릭스를 수정(Refine the camera matrix)합니다.
- 세련된 카메라 매트릭스(refined camera matrix)를 사용하여 이미지 왜곡 제거.
두 번째 단계는 getOptimalNewCameraMatrix() 메서드를 사용하여 수행됩니다. 이 세련된 매트릭스는 무엇을 의미하며 왜 필요한가요? 다음 이미지를 참조하십시오. 오른쪽 이미지에는 가장자리 근처에 검은색 픽셀이 있습니다. 이는 이미지의 왜곡되지 않은 현상으로 인해 발생합니다. 때때로 이러한 검은색 픽셀은 왜곡되지 않은 최종 이미지에서 원하지 않습니다. 따라서 getOptimalNewCameraMatrix() 메서드는 모든 검은 픽셀이 제외되도록 이미지를 자르는 데 사용할 수 있는 세련된 카메라 매트릭스와 ROI(관심 영역)를 반환합니다. 제거할 원치 않는 픽셀의 백분율은 getOptimalNewCameraMatrix() 메서드에 인수로 전달되는 매개변수 알파에 의해 제어됩니다.

방사형 왜곡이 높은 경우 alpha=0인 getOptimalNewCameraMatrix()를 사용하면 빈 이미지가 생성되는 경우가 있습니다. 이것은 일반적으로 방법이 가장자리의 왜곡에 대해 좋지 않은 추정치를 얻기 때문에 발생합니다. 이러한 경우 카메라를 다시 보정하고 이미지 경계에 가까운 다양한 보기로 더 많은 이미지를 촬영해야 합니다. 이렇게 하면 왜곡을 추정하는 데 이미지 경계 근처에 더 많은 샘플을 사용할 수 있으므로 추정이 향상됩니다.
Python code
# Refining the camera matrix using parameters obtained by calibration
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))
# Method 1 to undistort the image
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
# Method 2 to undistort the image
mapx,mapy=cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)
dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
# Displaying the undistorted image
cv2.imshow("undistorted image",dst)
cv2.waitKey(0)
C++ code
cv::Mat dst, map1, map2,new_camera_matrix;
cv::Size imageSize(cv::Size(image.cols,image.rows));
// Refining the camera matrix using parameters obtained by calibration
new_camera_matrix = cv::getOptimalNewCameraMatrix(cameraMatrix, distCoeffs, imageSize, 1, imageSize, 0);
// Method 1 to undistort the image
cv::undistort( frame, dst, new_camera_matrix, distCoeffs, new_camera_matrix );
// Method 2 to undistort the image
cv::initUndistortRectifyMap(cameraMatrix, distCoeffs, cv::Mat(),cv::getOptimalNewCameraMatrix(cameraMatrix, distCoeffs, imageSize, 1, imageSize, 0),imageSize, CV_16SC2, map1, map2);
cv::remap(frame, dst, map1, map2, cv::INTER_LINEAR);
//Displaying the undistorted image
cv::imshow("undistorted image",dst);
cv::waitKey(0);;
참고문헌
[1] J. Weng, P. Cohen 및 M. Herniou. 왜곡 모델 및 정확도를 사용한 카메라 보정
평가. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(10):965–980,
1992년 10월.
[2] 카메라 보정을 위한 OpenCV 문서.